CSC 558 - Predictive Analytics II, Fall 2024, Assignment 3 on nominal classification and ensemble models.

Assignment 3 due by 11:59 PM on Saturday November 2 via D2L Assignment 3.
There is the usual 10% reduction per day late and I cannot accept submissions
    after I go over the solution in class.

0. A little background from Gary Larson




My slides on MIDI and PCM (Pulse Code Modulation) Digital Audio.

MIDI Fanatic's Technical Brainwashing Center is the best site for MIDI specifications.
CSC220: Follow Technical Docs and Programming -> The MIDI Specification from that page.

1. To get the assignment:
Download compressed ARFF data files CSC558assn3_train_fulllag.arff.gz and CSC558assn3_test_fullag.arff.gz and Q&A file README.assn3.txt from these links.
You must answer questions in README.assn3.txt and turn it in to D2L by the deadline.

Each answer for Q1 through Q10 in README.assn3.txt is worth 10 points, totaling 100%.
There is a 10% late penalty for each day the assignment is late. It must be in before I go over the solution.

2. Weka and README.assn3.txt operations:
Start Weka, bring up the Explorer GUI, and open CSC558assn3_train_fulllag.arff.gz. Make sure to open the TRAIN data for training.
    Set Files of Type at the bottom of the Open window to (*.arff.gz) to see the input ARFF file. Double click it.
    Next, go to the Classify tab and set Supplied test set to CSC558assn3_test_fulllag.arff.gz. Make sure to use the TEST data for testing.

These are the attributes we will use in this analyze in CSC558assn3_train_fulllag.arff.gz and CSC558assn3_test_fullag.arff.gz.
We discussed time-series data analysis and this dataset on October 17.

@attribute movement numeric        # A movement of a musical piece, conceptually a song, numbered 0 through 3.
@attribute channel numeric            # A MIDI channel, conceptually a musician playing an instrument, numbered 0 through 3.
@attribute notenum numeric            # The note 0 through 127 being played. Think of a piano keyboard.
@attribute tick numeric                    # The time with the (movement, channel) sequence, needed for note lagging
@attribute ttonic numeric                 # The so-called "do note" or tonic or root, which is the key pitch of the scale.
                                                         # Initially ttonic is tagged data by the score generator.
                                                         # Handout code derives an empircal ttonic by taking the statistical mode of the notes
                                                         # played in a given (movement, channel).
@attribute tmode {Ionian,Mixolydian,Lydian,Aeolian,Dorian,Phrygian,Locrian,Chromatic} # scale being played



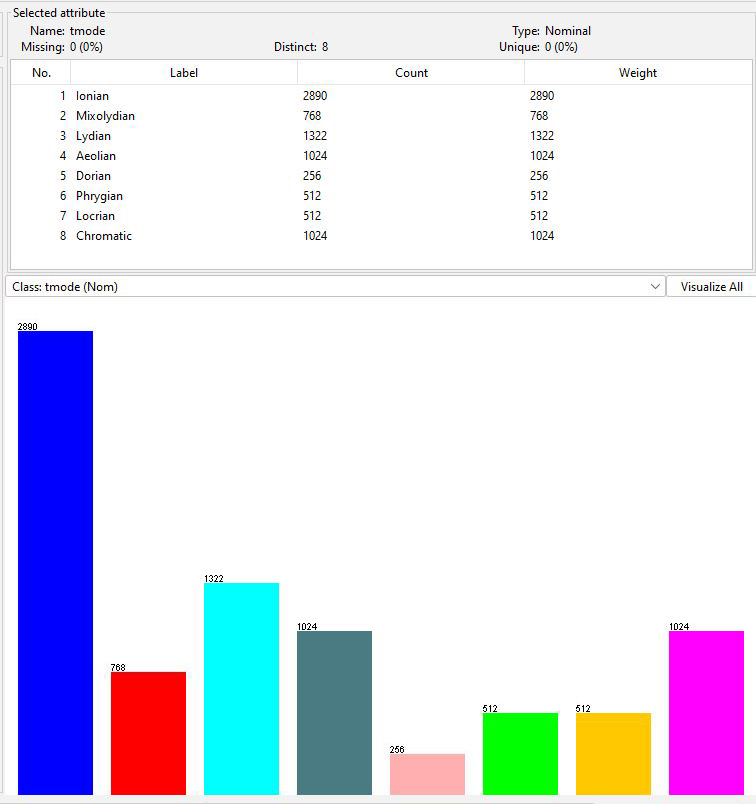
Figure 1: Distribution of tmode in the training dataset

We will classify tmode from other attributes. The test dataset has an identical but independent distribution to the training data. My genmidi.py Jython script generated training and testing data using different pseudo-random number seeds with distributions seen in that link. You do not need to understand the music theory in genmidi.py to do the assignment.



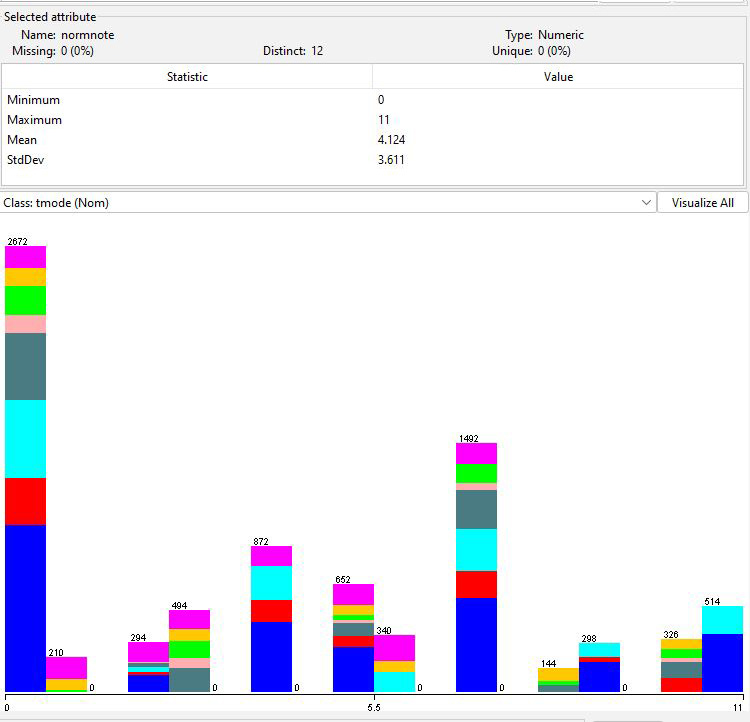
Figure 2: Distribution of normalized notes in the original data colored by correlation to tmode

In Figure 2 a normalized note is the note's distance from the tagged ttonic, which is the generator's intended "do" note in the tmode. My preparation script extracts an actual "do" note as the statistical mode (most frequently occurring value) of the normalized notes. Here is some diagnostic output from that script.

Computed and tagged tonic by (movement,channel):
('test', 0, 0) -> [7, 7]
('test', 0, 1) -> [7, 7]
('test', 0, 2) -> [7, 7]
('test', 0, 3) -> [7, 7]
('test', 1, 0) -> [9, 9]
('test', 1, 1) -> [9, 9]
('test', 1, 2) -> [9, 9]
('test', 1, 3) -> [9, 9]
('test', 2, 0) -> [7, 7]
('test', 2, 1) -> [7, 7]
('test', 2, 2) -> [7, 7]
('test', 2, 3) -> [10, 7]
('test', 3, 0) -> [7, 7]
('test', 3, 1) -> [7, 7]
('test', 3, 2) -> [7, 7]
('test', 3, 3) -> [7, 7]
('train', 0, 0) -> [7, 7]
('train', 0, 1) -> [7, 7]
('train', 0, 2) -> [7, 7]
('train', 0, 3) -> [7, 7]
('train', 1, 0) -> [9, 9]
('train', 1, 1) -> [9, 9]
('train', 1, 2) -> [9, 9]
('train', 1, 3) -> [9, 9]
('train', 2, 0) -> [7, 7]
('train', 2, 1) -> [7, 7]
('train', 2, 2) -> [7, 7]
('train', 2, 3) -> [1, 7]
('train', 3, 0) -> [7, 7]
('train', 3, 1) -> [7, 7]
('train', 3, 2) -> [7, 7]
('train', 3, 3) -> [7, 7]

All extracted tonics are the same as the tagged tonics except for these two:
('test', 2, 3) -> [10, 7]
('train', 2, 3) -> [1, 7]

This mismatch occurs because channel 3 uses a chromatic scale (mode) with uniform note distribution in movement 2, scattering notes with no pronounced tonic center. Channel 2 also uses a chromatic scale with uniform note distribution in movement 2. Channels 0 and 1 use more constrained modes but with uniform distribution in movement 2. Movements 0, 1, and 3 use Gaussian generation of notes in the tmode, generating more predictive notes for each target mode.

Handout file CSC558assn3_train_fulllag.arff.gz and CSC558assn3_test_fullag.arff.gz also contain these derived attributes. These are counters added from the current time's notenum and the temporally preceding 11 instances within a given (movement, channel) in temporal order sorted by tick values.

@attribute lagNote_0 numeric
@attribute lagNote_1 numeric
@attribute lagNote_2 numeric
@attribute lagNote_3 numeric
@attribute lagNote_4 numeric
@attribute lagNote_5 numeric
@attribute lagNote_6 numeric
@attribute lagNote_7 numeric
@attribute lagNote_8 numeric
@attribute lagNote_9 numeric
@attribute lagNote_10 numeric
@attribute lagNote_11 numeric

These are histogram sums of intervals in one scale with the ttonic at lagNote_0 being the extracted ttonic and the others being steps on the piano above that, up to but not including the next octave.

Each of lagNote_0 through lagNote_11 is the lagged notenum from up to
previous 12 instances (determined by measuring maximum kappa
fed back from _main.py module) within the current (movement, channel),
lagged by previous notes. "lagNote_0" is the count of tonic notes within the
lag period, and "lagNote_11" is the count of "major 7ths" within the lag
period. You do not need to understand music theory, only the fact that
the distribution of counts in the lagNote_0..lagNote_11 correlates
to the tmode (scale) which is the target attribute. Knowing attributes
movement, channel, notenum, tick, and ttonic is like reading the
musical score.

From the Python script that aggregates movement-channel
note sequences into the lagged attributes:
# From a "backInTime" time lag of 0 up through "backInTime" of -12,
# copy lagged preceding (in time) normalized (w.r.t. extracted tonic)
# into the current instance, stopping before "bakInTime" of -12 if
# a peak in kappa is passed, i.e., passing point of diminishing
# returns on kappa. Derive two "kappa-optimized" datasets as follows.
#
# trainNonTargetData, testNonTargetData use all attributes including
# movement, channel, ticks, etc., through the lagged note histograms.

Here are genConcert_train.arff.gz and genConcert_test.arff.gz containing
the original (movement, channel) note streams before lag aggregation.
The figure below shows the Ableton Live software mixer with the generated
MIDI piano roll for Chromatic movement 2 channel 3. A video demo is here. Updated 10/17.




Ableton Live software mixer with the Generated note streams before lagging


3. Perform the steps and answer all Qn questions in README.assn3.txt and turn in via
D2L Assignment 3 by the due date.