Tutorial 25:
Standard Time
Concepts:  We saw in Tutorial 21 that time and longitude are intimately related.  Local Solar Time (LST), as we where shown, may vary by hours, minutes, and even seconds.  If we were to live on LST, we would have to keep readjusting our watches for every town we stopped at while traveling east or west.  That would not be practical.  What we really need is to establish wide areas or zones that share the same time.  What we need to do is standardize time.

Facts:

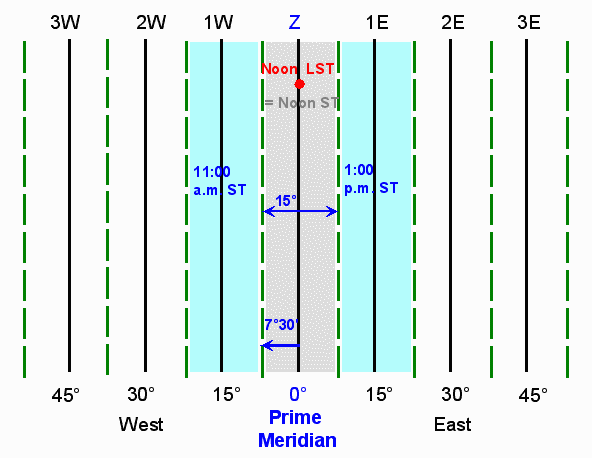
1) There are 24 time zones, one for each hour of the day.

2) Since these zones must cover all of a sphere, which is a full 360° around, each zone must be 15° wide.

3) The middle of each zone contains a Standard or Central Meridian.

4) Each zone middle is spaced 15° apart.  Zone edges are therefore 7°30' on either side of their respective central meridians.

5) Zones are counted as one travels away from the Prime Meridian which is 0° longitude.

6) Since zone middles are in increments of 15°, one may easily determine the middle of any zone.  For instance, the middle of zone 3 west will be 3 increments of 15° to the west of the prime meridian or 45° west.
 

How is Standard Time Determined? Standard Time (ST) is related to Local Solar Time (LST).  When it is noon LST, for instance, for a central meridian (like shown above), it becomes noon standard time for the entire zone.  Whenever one crosses a zone edge (always shown as dashed lines) into a new zone, the standard time must change by one full hour (see the diagram above).

Hint:  On exams, if the problem is Standard Time related, any answer that differs by minutes and/or seconds must be wrong.  Standard time always varies by full hour increments.

How to do Standard Time Problems:  Here are some helpful steps to follow.

1) Since zone middles are all increments of 15° away from the Prime Meridian (0°), we may estimate which zone any longitude is in by dividing its degrees of longitude by 15.

2) If, when you divide a location's degrees of longitude by 15, the decimal is less than 0.5, you must draw the zone to see if the location falls within the estimated zone.

3)  If the decimal is greater than 0.5, then the location is in the next zone.

4)  If the decimal is .0, then the location lies essentially in the middle of the estimated zone.
 

The decimal rules are proven below.
 
In which zone would a place 46°40' W be located?



 
 
 
 

In dividing the number of degrees (46) by 15 we get 3.02.  We have estimated that our location is in zone 3 west or z3w.  We need to determine if our location is still within z3w.
 
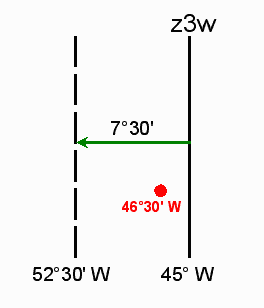
We need, then, to determine the western edge of the zone and then plot our location.  The western edge of the zone is another 7°30' to the west or at 52°30W.  When we plot 46°30'W, we see that it falls easily within z3w.
 
 
 
 
 
 
 
 
 
 
 
 
In which zone would a place at 37°59'W be in?



 
 
 
 

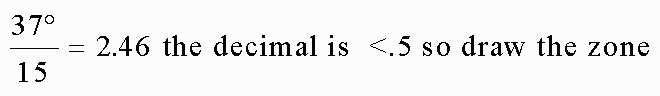
The estimated zone is z2w.  The middle of z2w is 30° W and its western margin is another 7°30' west.



 
 

In this instance, the destination falls in the next zone, z3w, even though the decimal is less than .5 like in the previous example.  You MUST draw the estimated zone whenever the decimal is less than .5.
 
 
 
 
 

In which zone would a place 41°20'E be in?


This time when we divide the number of degrees by 15°, we get a decimal greater than 0.5.  This means that our location is in the next zone.



 
 

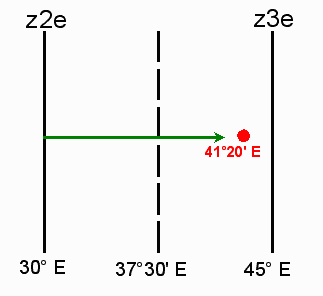
The whole number 2 shows that we have crossed the middle of z2e which is two increments of 15° or 30° east.  The eastern margin of the zone is 37°30'E.  When we plot our location, we can clearly see that it is in the next zone.  The answer is z3e.

 
 
 
 
 
 

Sample Problems: There are essentially two types of standard time problems we may face.  When given the longitudes of two locations, we should be able to figure out how many zones separate them and therefore the number of hours their times differ.  Or, we may be given the standard time in two places and be expected to figure out how many zones are between them.  These problem types are shown below.

1) What will the time be at 53°27'E if the day and time are Tuesday 5:30 p.m. ST at 75°21'e?
a. First determine whether the destination is east or west of the known.  In this instance, the destination is west of the known.  You automatically know that the time at the destination will be earlier.

b. Now determine in which zone each place is located.  Use the technique shown above.

There is only one zone between our two locations so their standard times will only differ by one hour.  The time and day at 53°27'E is 4:30 p.m. Tuesday ST.

2) What zone will be experiencing 3:30 p.m. Monday ST if the time is 12:30 p.m. Monday ST at 83°27'W?
a. Since the time is later at our destination, it must be to the east of our known.

b. Determine the zone of our known.
 

c. Since the time difference is three hours, the destination must be three more zones to the east.  The answer is zone 3 west (z3w).
 

The examples you have just seen all assume that time zones are a constant 15° wide.  In reality, the choice of what zone a particular place is in is a political decision.  Such choices alter the sizes and shapes of zones.  Take a look at the map of the zones in the lower 48 states.

The four zones that cover the lower 48 states are based on the 75°, 90°, 105°, and 120° central meridians.  The zone edges should be straight lines 7°30' on either side of the shown central meridians.  Look at the Eastern time zone (in the darker blue on the right).  Its edge is highly irregular...politics, politics, politics.  The zone's border reflects the political decisions of the states in the eastern third of the country.  Ohio belongs in the Eatern zone, but look at its neighbor to the west.  Which state is that anyway?  That state is in the wrong zone!  It should be in the Central zone.  Make sure to become familiar with the names of the zones in the US shown on this map.
 
 
 
 
 



 
 


 
 

Now look at the world map of time zones.  What a mess!  The shapes are irregular and some zones have time offsets that include half-hour differences (see India for example).

Remember that when we do zone calculation problems, we are always assuming simple, perfect, even, ideal zones and not the mess we see in reality.
 
 
 
 
 
 
 

 
 

Daylight Saving Time: As the time of year approaches summer (which begins on the June Solstice for us in the Northern Hemisphere), we notice that the sun progressively rises earlier and earlier and sets later and later in the day.  Overall, daylight hours increase to their maximum on the June Solstice.  To make it that the sun doesn't rise too early (4:30 a.m. for example), and to extend daylight later into the afternoon/evening, we have adopted Daylight Saving Time (DST).  On the first Sunday in April, clocks are set ahead by one hour over standard time (ST).  For example, 2:00 a.m. Sunday, becomes 3:00 a.m. Sunday.  You've lost an hour of sleep!!  This also means that on the June solstice, the sun will rise at 5:30 a.m. instead of 4:30 a.m.  Daylight Saving Time ends on the last Sunday of october; time "falls back."  For example, 2:00 a.m. DST becomes 1:00 a.m. ST; you've gained an hour of sleep...I love that!
 

Calculating Daylight/Nighttime Hours

So what time is it anyway?  Follow this link to the official time web site of the United States Government and find out!