Tutorial 16:
Lapse Rates and Orographic Precipitation
Concept:  Orographic precipitation involves air being forced to rise over a mountain.  We know that as air rises its temperature will drop adiabatically.  We also know that air's water vapor holding capacity (SMR) diminishes as it cools.  Further, if the SMR drops, relative humidity (RH) increases.  The idea is that if air is forced to rise over a mountain the air will cool, the SMR will drop, the RH will increase and dew point (DP) may be reached.  If DP is reached and the air is forced to rise and subsequently cool further, precipitation will occur.  Precipitation occurring as a result of air being forced to rise over a mountain is called Orographic Precipitation.

Operationalization:  We may calculate how much air changes temperature as it is forced to go up and over a mountain since we already know the Dry Adiabatic Lapse Rate (DALR) and the Saturated Adiabatic Lapse Rate (SALR).  Guess what; that is exactly what I expect you to be able to do on an assignment and on any exam!  Don't despair, there are only two types of problems that you may face.  Either you will solve for a temperature change given a distance over which air rises, or you may solve for a distance given a temperature change.  Both types of problems are shown below.

1) Air approaching on the windward side of the mountain begins at 17°C and is forced up the mountainside.  The air cools as it rises and eventually reaches dew point at an altitude of 400m.  Find the Dew Point Temperature (a).
Solution:  Here you know a distance (a 400 meter rise) and need to translate that into a temperature change.  You also know that the air rising is "dry" because the original air is NOT a cloud.  What you need to do is figure out how much dry air will cool over a 400m rise (see below).
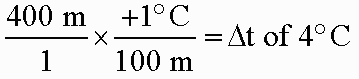
The air will cool by 4°C from a beginning temperature of 17°C so the dew point temperature must be 17°- 4° = 13°C.
2) The air continues to rise over the mountain and cool.  The air cools to 10°C by the time it reaches the summit.  Can you figure out how high the top of the mountain is (b)?
Solution:  You need to find out the distance from the base of the cloud to the top of the cloud.  If you add that distance to the distance the cloud base is above the ground, you will have the total mountain height.  How do you figure the cloud's depth?  You know the base of the cloud is at 13°C and the cloud's top is at 10°C.  This is a 3°C temperature drop at the SALR.  You must use the SALR because we have cloud.  Translate the temperature change to a distance.
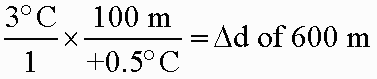
So, if you add the 400m cloud base height to the 600m from the base of the cloud to the mountain top, you get a total distance of 1,000m or 1km.
3) Now solve for the air temperature a the leeward base of the mountain (c).  Remember that whenever air descends, it warms adiabatically.
Solution:  The distance from the mountain top to the leeward base is 1km.  So the 1km distance needs to be converted to a temperature change.  Remember also that we use the DALR whenever air descends.  The change in temperature is calculated as follows.
The air will warm by 10°C over the 1km distance.  Since the air began at 10°C and warmed by the same amount, the temperature at the leeward base will be 10° + 10° =  20°C.
The Rainshadow Effect:  When condensation occurs on the windward side of a mountain, as shown above, conditions on the leeward side will we warmer and drier.  The reason why conditions will be warmer is because of the fact that when air reaches dew point, condensation occurs.  The condensation process involves the conversion of latent heat to sensible heat; clouds warm themselves as they form.  This release of sensible heat partially offsets the adiabatic cooling process.  Therefore, by the time the air reaches the top of the mountain it will be warmer than if condensation had not occurred.  The descending air will then warm all the way down the leeward side of the mountain at the DALR (the fast rate) (see the calculations above).  If condensation was not indicated on the diagram above, air would cool at the DALR all the way to the top and then all the way back down the leeward side; temperatures on the windward and leeward sides would be the same!!  See if you can prove this.  Just remove the cloud and mark the elevation of the mountain top 1 km.  What would the temperature be at the mountain top then and what would the new temperature be at the leeward base?
The conditions on the leeward base would also be drier than at the windward base.  Since precipitation occurred on the windward side, the AMR would have dropped from what it was at the windward base (I do not show AMR on the diagram above...you'll have to trust me on this one until we do a problem that proves this in class).  The drier air descending the leeward side will warm adiabatically, its SMR will increase, and the RH will drop, and precipitation will not occur.  This forms a "rainshadow" on the leeward side.  People living on the leeward sides of mountains will commonly notice very hot, dry winds descending the leeward side because orographic precipitation is occurring on the windward side.  These winds are referred to as Chinook Winds on the eastern side of the Rocky Mountains.