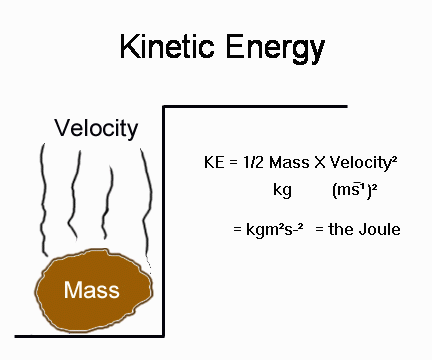
I Potential Energy:

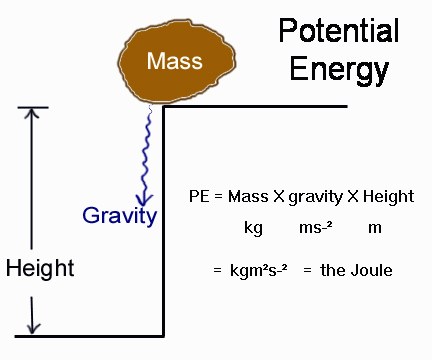
If you think about it, you intuitively know that an object suspended above the ground and in the earth's gravitational field must have energy stored in it. How about a 16lb. bowling ball suspended 3.5 feet above your foot? You know that if you drop the ball gravity will cause the ball to fall and smash your foot. OUCH! Work has just been done on your foot. Where did the energy come from? Your arm lifting the ball performed work. Remember that energy may neither be created nor destroyed so the work your arm performed and the energy you expended must be somewhere…in the bowling ball sitting stationary some distance above the ground. Since you cannot detect the energy stored in the ball, we consider the energy to be potential in nature. A mass suspended in a gravitational field some distance above a surface contains Potential Energy (PE).

                    PE = Mass x gravity x Height; g = 9.81ms^-2

            Checking units: Kg x ms^-2 x m = kgm²s^-2 = the Joule

Metric mass units are in kg, gravity is ms^-2, and height is in m. Always track units!!  When you are doing energy calculations, you must end up with the Joule.

The diagram below depicts a situation where potential energy is present. Here we have a mass suspended in a gravitational field some height above a surface. If you commit this diagram to memory, you should always be able to remember the formula for Potential Energy.

Example: How much potential energy will be stored in a 30 pound boulder suspended in the earth's gravitational field 30 feet above the ground?

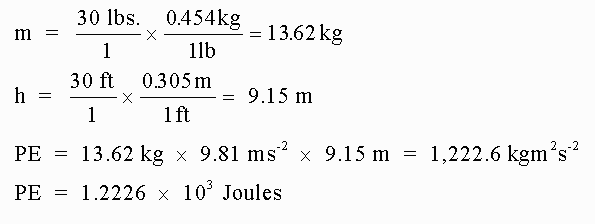
II Kinetic Energy:

If a quarterback throws a football, a mass has been accelerated over a distance. This means that work has been performed and therefore energy has been expended. Where did the energy that the quarterback expended go? The energy can only be in the moving mass of the football. If it were to hit you on the nose, you would come to the conclusion that the football just did work on your face. The energy stored in a moving mass is called Kinetic Energy (KE).

                        KE = 1/2 Mass x Velocity²

                Checking units: kg (ms^-1)² which equals kgm²s^-2 or the Joule.

If the boulder in the diagram above were to fall, all of the potential energy stored in the boulder would be turned into kinetic energy or speed. The following diagram shows that there are only two variables involved in kinetic energy, mass and velocity. Commit this diagram to memory too.