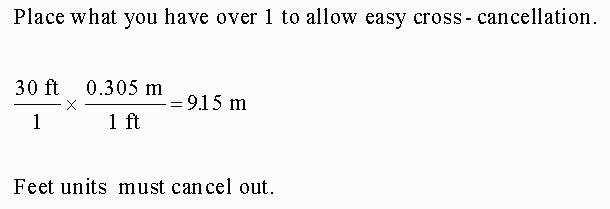
An exponent or "power" indicates how many times a number is to be multiplied by itself.  For instance, 2 to the power of 3 (2³) means 2 x 2 x 2 or 8.  Another example might be 4 squared, or 4², which means 4 x 4 or 16.

Exponents or powers may be positive, as shown above, or negative.  Whenever a number is raised to a negative exponent like 4^-2, it means one over the expression.  Therefore, 4^-2 becomes 1/4² or 1/(4 x 4) or 1/16.  Another example might be 5^-3 or 1/(5 x 5 x 5) or 1/125.  Six to the negative first power (6^-1) is 1/6.

There are some special exponents.  Any number raised to the first power is unchanged.  For instance, 4¹ is simply 4.  Since the first power doesn't change a number, the first power is not usually shown on numbers; the first power is implied.  Any number raised to a power of zero is one.  This is because:
X⁰ = X^n-n = Xⁿ x X^-n = Xⁿ/Xⁿ = 1. So, 99⁰ = 1.

Units may also be raised to powers just as numbers may be.  When calculating area, one multiplies the lengths of two sides of a square.  If a square is 2 meters by 2 meters, then the area of the square would be calculated as 2m x 2m which yields 4 m x m or 4m².  A plateau measuring 2 miles by 4 miles would have an area of 8 square miles or 8mi².  Volume is calculated by multiplying the lengths of three sides of a three dimensional object.  So the volume of a cube measuring 1m x 1m x 1m would be 1 m x m x m or 1m³.  A tide pool measuring 2ft wide by 3ft long by 2ft deep would have a volume of 12ft³.  If 200 people lived in a one square mile (1mi²) area, then we could figure the population density of the area.  Density is a count over an area so 200 people/1mi².  Remember that a negative exponent means 1 over something...so, the density would be 200people mi^-2.  This would be read as, "Two hundred people per square mile."  Notice that the negative exponent translates verbally to the word per.
 

II Scientific Notation:

Scientific notation is a means of expressing very large or very small numbers in a simplified fashion.  The basic format is to convert the original number to one between 1.0 and 9.9 and to multiply it by ten raised to some exponent.  Multiplication by ten only serves to move the decimal.  For instance, the number 135,000 (a number greater than 1) would be converted to 1.35 first.  This follows the rule to express numbers between 1.0 and 9.9.  Note that we had to move the decimal five decimal places.  This means that we must multiply 1.35 by ten to the fifth power or 1.35 x 10⁵.  The number 5,000,000 would become 5.0 x 10⁶.  Again, the original number was greater than one so the power is positive.  The number 230 becomes 2.3 x 10².

If you are given a number is scientific notation, you will be expected to be able to convert it to longhand. For instance, convert 3.67 x 10⁴.  This number has a positive exponent so the longhand version should be greater than one.  Note that if we moved the decimal the prescribed four positions but to the left, the number would become 0.000367 which would be SMALLER than one.  We would have moved the decimal in the WRONG direction.  To keep the number greater than one, as a positive exponent indicates, we must move the decimal four positions to the right yielding 36,700.

Very small numbers may also be expressed in scientific notation.  For instance, convert 0.00034.  This number is less than one so we automatically know that the exponent will be negative!  So, make the number between 1.0 and 9.9 (3.4) and then use a negative exponent that records how many places the decimal had to be moved (-4).  The number properly expressed in scientific notation becomes 3.4 x 10^-4. Likewise, 0.0000984 would become 9.84 x 10^-5.  What does 7.77 x 10^-3 mean?  Answer; 0.00777, a number less than one.
 

III Metric System:

Basic Units

There are essentially three basic units of measure; mass, length, and time. Standard units for these measures are the pound (lb.), the foot (ft.), and the second (s).  In metric, the units are the gram (g), the meter (m), and the second (s).  From these units one may create "derived" units.  For example, area, volume, and density are multiples or combinations of units so they are considered to be derived.  Velocity (or speed) is another.  Your car’s speedometer gives your velocity, the distance you travel over a given time period, in MPH. What does that mean?  MPH is short for miles per hour.  Do you remember what the word per translates into?  Let’s see. MPH means mihr^-1.  In metric we use kilometers per hour or kmhr^-1. We also use meters per second or ms^-1.

Conversions

You must be able to convert between the standard and metric systems.  To do this, we will use several conversion factors or what are known as "Factors of One."  For instance, there are 0.305 meters to one foot or 0.305m/ft.  Since 0.305 meters is the same length as one foot, the conversion factors as a fraction is equal to one.  This also means that the factor may be "flipped over" and it will still be true; 1ft/0.305m.  This means that you only need one conversion factor to go from feet to meters or from meters to feet. A list of needed conversion factors is given on Exercise One.

When doing conversion problems you should always use and keep track of units.  If unwanted units cross cancel and leave the units you desire, then you know that you have setup the problem correctly.

Convert 30 feet to meters:

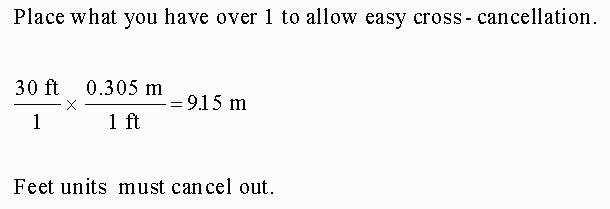
 Put what you have, 30ft, over 1 to allow for cross cancellation of unwanted units.  Now put in the conversion factor in a way that will cause ft to cancel out.  Then multiply straight across.

Convert 75 meters to feet:

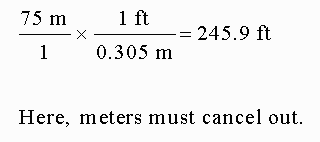
The procedure is that same as before, but you had to flip over the factor to allow meters to cancel out.  This one just needed division.

Convert 60 kilograms to pounds:

Convert 25 pounds to kilograms:

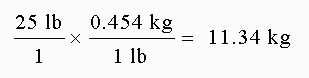
Convert 60 miles per hour to kilometers per hour:

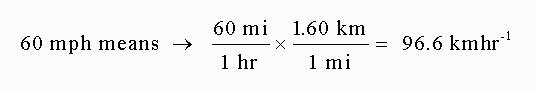
 Convert 30 kilometers per hour to miles per hour:

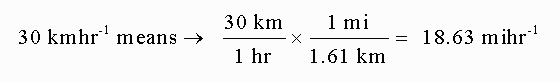
Multiplying Prefixes

The basic metric units discussed above may be altered using multiplying prefixes.  If a unit is too small it may be re-expressed as multiples of the same unit.  Likewise, if a unit is too large it may be re-expressed as fractions of the same unit.  A few of such multiplying prefixes are found below.

Prefixes for multiple units:

    M for mega means 1 x 10⁶ units. 2Mm means 2,000,000m.

    k for kilo means 1 x 10³ units. 30kg means 30,000g.
 

Prefixes for fractions of units:

    c for centi means 1 x 10^-2 units. 2cm means 0.02m.

    m for milli means 1 x 10^-3 units. 45mg means 0.045g.

     µ for micro means 1 x 10^-6 units. 3 µm means 0.000003m.
 

Convert 1 mile to centimeters:

First convert miles to kilometers and then km to cm.
 

Convert 30 miles per hour to meters per second (ms^-1).

Temperature Scales:

We need to be familiar with three temperature scales: Fahrenheit, Celsius, and Kelvin.  The graphic below shows some important marker temperatures and how the three systems relate.

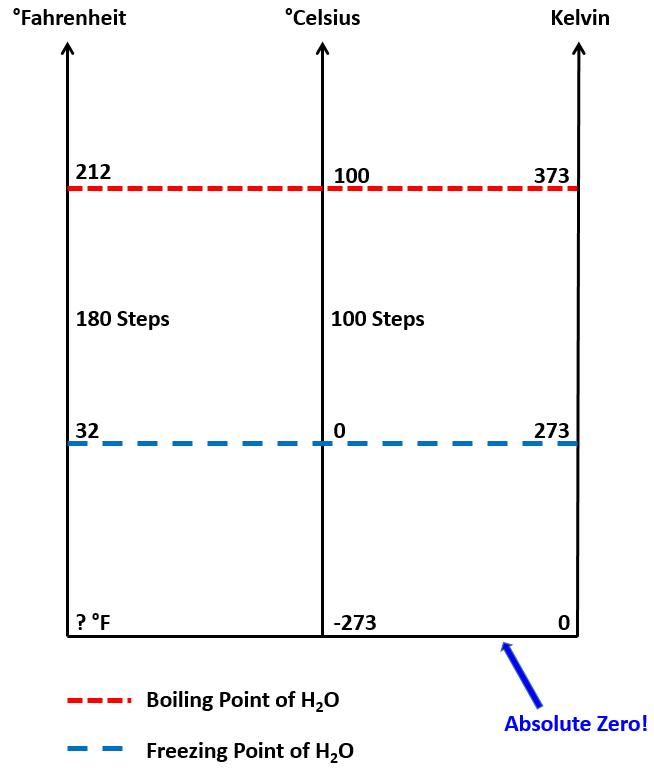Note that to go from freezing to boiling on the °F scale takes 180 steps and only 100 steps on the °C scale.  This means that the Celsius degree is 1.8 times larger than the Fahrenheit degree.  The Kelvin system is based on Absolute Zero and thus has no negative values.  Absolute Zero in °C is -273.  The Kelvin and Celsius units are the same, so freezing in Kelvin is 273, and boiling is 373.

Temperature Conversion:

We must be able to convert between Fahrenheit (°F) and Celsius (°C).

                    Convert 75°F to °C:

                                                            °C = (75 – 32) / 1.8 = 43 / 1.8 = 23.9°

Remember to do the subtraction first!!
 

                    Convert 20°C to °F:

                                                            °F = (1.8 x 20) + 32 = 36 + 32 = 68°

Here you must do the multiplication first!!